Linear versus Nonlinear FEA: What’s the Difference?

Table of Contents

 

Introduction

In the field of engineering and structural analysis, Finite Element Analysis (FEA) is a widely used method for solving complex problems. (Click here to learn more about the advantages of using FEA.) FEA can be categorized into two fundamental approaches: “linear” and “nonlinear.” I’ve found over the years that these terms are often misunderstood. For this reason, this article looks at linear versus nonlinear FEA, unveiling the key differences, shedding light on the essential disparities between these two analytical methods, and looking at the advantages and disadvantages of each.

Linear FEA assumes that the relationship between the applied loads and the resulting displacements is linear, meaning that the response is proportional and predictable. For example,  a linear FEA assumes that if a one-pound load applied to a structure produces a 1-inch deflection, then a 10-pound load will produce a 10-inch deflection in that same structure. On the other hand, nonlinear FEA takes into account the nonlinear behavior of materials and structures, where the relationship between the applied loads and displacements is not proportional and can exhibit complex behavior.

By understanding these differences, engineers and analysts can make informed decisions about which method to use depending on the complexity of the problem at hand.

 

Linear FEA: Definition and Principles

For a linear Finite Element Analysis to be valid the following three assumptions must be true:

1. Material Linearity – Material linearity refers to the behavior of a material under load. A linear elastic material, such as steel, follows Hooke’s law and the geometry of the material will return to its original shape once the load is removed. This behavior is characterized by a stress-strain curve that is predominantly linear, as shown in the stress-strain curve for steel.

The stress-strain curve for linear materials like steel shows a nearly straight line up to a certain point, known as the yield point. During this linear region, the relationship between stress (force per unit area) and strain (deformation) is consistent and predictable.  (The slope of this line is the material’s Young’s Modulus.) However, beyond the yield strength, the stress-strain curve is no longer linear.

To put it succinctly, linear materials like steel exhibit a linear stress-strain relationship until they reach their yield strength. Beyond this point, the material no longer follows a linear pattern, rendering linear Finite Element Analysis (FEA) inappropriate for analyzing stresses that exceed the material’s yield strength.  Fortunately, most engineering problems are concerned with stresses below the yield point, as products with stresses near or above yield are typically considered to be failures, or at the least, to have an inadequate factor of safety.

2. Geometric Linearity – Geometric Linearity hinges on the assumption that a structure’s stiffness remains unchanging as loads are applied. This premise remains valid when deformations are “small” relative to the overall dimensions of the model. However, determining what qualifies as “small” is not always straightforward or intuitive, as illustrated in the examples later in this article. Seasoned FEA users often rely on their expertise, but occasionally, conducting a comparative analysis of linear and nonlinear FEA results may be necessary to precisely ascertain the degree of deformation that can be considered “small.” Even a small deformation, if it causes two separate parts to come into contact, will cause a nonlinearity that can render the linear FEA invalid.
3. Linear Boundary Conditions – This assumption presumes that all applied loads and constraints remain constant in magnitude and direction throughout the entire analysis.

If any of the three above assumptions is not valid, the linear FEA will not be valid and a nonlinear FEA will be needed to get reliable results.

One of the main advantages of linear FEA is its computational efficiency. Since linear FEA involves solving linear equations, the analysis can be performed relatively quickly compared to nonlinear FEA. Additionally, linear FEA provides accurate results for systems that exhibit linear behavior, making it a reliable and widely used method in engineering practice.

However, linear FEA has its limitations. It cannot accurately capture the behavior of structures under large deformations, material nonlinearity, or geometric nonlinearity. In such cases, nonlinear FEA methods are required.

 

Nonlinear FEA: Definition and Principles

Nonlinear Finite Element Analysis (FEA) is a computational method used to solve complex engineering problems that involve nonlinear material behavior, large deformations, and contact interactions. Unlike linear FEA, which assumes that the relationship between the applied loads and the resulting deformations is linear, nonlinear FEA takes into account the nonlinear behavior of materials and the nonlinear response of structures under load.

In linear FEA, the governing equations are linearized, allowing for a relatively straightforward solution. However, in many real-world scenarios, the linear assumptions outlined in the section above are not valid, and nonlinear FEA becomes necessary to accurately predict the behavior of structures and materials.

Nonlinear FEA involves solving a set of nonlinear equations iteratively until convergence is achieved. This iterative process accounts for the nonlinearities in the problem, such as material nonlinearity (e.g., plasticity as shown in the stress-strain curve for polypropylene and hyperelasticity) and geometric nonlinearity (e.g., large deformations, contact). The solution obtained from nonlinear FEA provides a more realistic representation of the system’s behavior under complex loading conditions.

One of the key principles of nonlinear FEA is the use of incremental analysis. Instead of solving the entire problem at once, the analysis is divided into small increments, and the solution is obtained incrementally. At each increment, the equilibrium equations are solved, and the updated state of the system is determined. This incremental approach allows for the consideration of nonlinear effects and ensures the accuracy of the solution.

 

 Advantages of Linear FEA

Linear Finite Element Analysis (FEA) offers several advantages that make it a popular choice for many engineering and simulation applications. Here are some key advantages of linear FEA:

1. Simplicity: Linear FEA is relatively simple to implement compared to nonlinear FEA. The mathematical equations used in linear FEA are linear, which means they can be solved using well-established techniques and algorithms.
2. Computational Efficiency: Linear FEA requires fewer computational resources compared to nonlinear FEA. Since the equations are linear, the solution process is faster and requires less memory. This makes linear FEA suitable for analyzing large-scale structures or systems where computational efficiency is crucial.
3. Stability: Linear FEA is inherently stable and predictable. The linear equations used in the analysis have unique solutions, and the behavior of the system can be accurately predicted. This stability is particularly important in engineering applications where accurate predictions are necessary for design optimization and safety considerations.
4. Validity for Small Deformations: Linear FEA is well-suited for analyzing systems with small deformations. In cases where the deformations are within the linear range, linear FEA provides accurate results. This makes it suitable for applications such as structural analysis, where the deformations are typically small compared to the overall size of the structure.
5. Linear Superposition: One of the key advantages of linear FEA is the principle of linear superposition. This principle allows engineers to analyze complex systems by breaking them down into simpler components and analyzing them individually. The results from these individual analyses can then be combined using linear superposition to obtain the overall response of the system. This makes linear FEA a powerful tool for analyzing complex structures and systems.

Linear FEA’s simplicity, computational efficiency, stability, validity for small deformations, and the principle of linear superposition make it suitable for a wide range of applications. It is for these reasons that Linear FEA accounts for the vast majority of FEA.  At Situs Engineering, approximately 90% of the FEA services we provide for our clients are Linear FEA.

 

Advantages of Nonlinear FEA

Nonlinear Finite Element Analysis (FEA) offers several advantages over its linear counterpart, making it a valuable tool in various industries. Here are some key advantages of nonlinear FEA:

1. Accurate representation of complex material behavior: Linear FEA assumes that the material properties remain constant throughout the analysis. However, in many real-world scenarios, materials exhibit nonlinear behavior, such as plastic deformation, large displacements, or material softening. Nonlinear FEA can accurately capture these complex material behaviors, providing more realistic and accurate results including material behavior, such as plasticity, creep, and hyperelasticity.
2. Ability to handle large deformations: Linear FEA is limited to small deformations, where the relationship between the applied loads and resulting displacements remains linear. Nonlinear FEA, on the other hand, can handle large deformations and nonlinear relationships between loads and displacements. This makes it suitable for analyzing structures subjected to significant deformations, such as rubber components, metal forming processes, or crash simulations.
3. Capturing geometric nonlinearity: Linear FEA assumes that the geometry of the structure remains unchanged throughout the analysis. However, in many cases, the geometry may undergo significant changes due to large deformations or contact interactions. Nonlinear FEA can accurately capture these geometric nonlinearities, allowing for more realistic simulations.
4. Simulation of contact and friction: Nonlinear FEA enables the simulation of contact and friction between different parts of a structure. This is crucial in analyzing assemblies or mechanisms where parts come into contact with each other, such as gears, bearings, or joints. By considering contact and friction effects, engineers can evaluate the performance and durability of these components more accurately.
5. Improved accuracy and reliability: Due to its ability to capture complex material behavior, large deformations, geometric nonlinearities, and contact interactions, nonlinear FEA can provide more accurate and reliable results compared to linear FEA. This is particularly important in critical applications where small errors can have significant consequences.

Nonlinear FEA offers several advantages over linear FEA, allowing for more accurate and realistic simulations when the assumptions required for a linear analysis cannot be met.  However, this increased accuracy comes at a cost.  Nonlinear FEA requires more computational resources (requiring more time and money to complete the calculations). Nonlinear FEA can have convergence issues that cause the FEA solver to fail. It requires more complex material models.  (A linear analysis requires only the material’s Young’s modulus and Poisson’s ratio, while a nonlinear analysis requires a full stress-strain curve which can be difficult to find for some materials.) And, nonlinear FEA requires a higher level of expertise and training compared to linear FEA.  All of this adds up to nonlinear FEA being considerably more expensive than linear FEA.

Linear versus Nonlinear FEA – Which One Do I Need?

After reading the above information, you may still wonder which type of FEA you need for your project.  If the three assumptions of material linearity, geometric linearity, and boundary condition linearity outlined in the Linear FEA: Definition and Principles section above are true, then a linear FEA solution should be valid.  And, due to the efficiency and cost benefits of the linear analysis over a nonlinear analysis, the linear analysis is generally the preferred method.  However, there are many instances where it is not abundantly clear whether or not a linear FEA is adequate.  In this section, we’ll look at just a couple of scenarios that I have seen cause some confusion.

Case 1: Membrane Structures

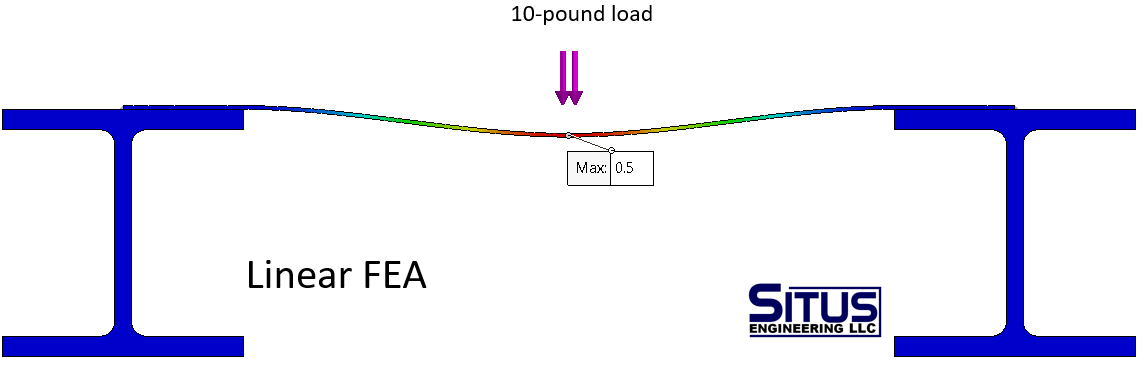
FEA problems involving membrane stress (i.e., the stress acting along the thickness of thin material) typically necessitate the use of nonlinear FEA to get reliable results even when the material is a linear material and the deformations are “small”.  Consider the simple analysis shown below of a 1-pound load placed on a piece of thin steel sheet metal that is welded to two rigid structural members.  The load is constant (i.e., boundary condition linearity), the material is a linear material and its stresses remain below the yield stress of the material (i.e., material linearity), and the deformation seems small (i.e., geometric linearity), so this seems to meet the conditions for a reliable linear FEA.

The linear FEA above shows a deflection in the sheet metal, which is very thin and offers little resistance to bending, to be 0.05” under the 1-pound load.  The nonlinear FEA shows the same 0.05” deflection.

Now, if we amplify the load by a factor of 10, our anticipation in a linear analysis is that the deflection will correspondingly increase by a factor of 10, resulting in a deflection of 0.5 inches. This deformation still appears relatively modest, and as validated by the linear FEA results presented below, the displacement has indeed escalated by a factor of 10, reaching 0.5 inches.

However, this outcome is erroneous because linear FEA fails to consider the emergence of membrane (in-plane) stresses as the sheet metal undergoes stretching beyond its initial bending. The linear analysis maintains geometric linearity and does not recalculate the stiffness throughout the analysis, leading to an inaccurate prediction of the increased deflection.

In contrast, nonlinear FEA employs an incremental approach. Rather than attempting to solve the entire problem in one go, the analysis is broken down into small increments or time steps. At each increment, the equilibrium equations are solved, and the system’s stiffness is updated accordingly to account for the stresses required to stretch (not just bend) the material. This incremental process ensures a reliable result in cases like this one, where the deformation is not adequately addressed by linear analysis.

As shown in the nonlinear FEA results below, the actual deflection is only 0.1”.  Therefore, the linear FEA overestimated the displacement by a factor of five and did not produce reliable results.

 

Case 2: Plastic Materials

By definition, plastic materials such as polypropylene exhibit plastic behavior, not linear elasticity behavior, and therefore, they do not satisfy the material linearity prerequisite for linear FEA validity. However, it’s essential to note that this technical distinction doesn’t imply that linear FEA lacks usefulness in assessing plastic components.

Taking a closer look at the stress-strain curve for polypropylene, we observe that, despite the material’s nonlinear nature, certain portions of the curve can be reasonably approximated by a straight line. The slope of this line represents the material’s Young’s modulus in this stress range. As long as the applied stresses in the analysis remain within the range of this straight-line approximation, we can obtain relatively accurate results using linear FEA with Young’s modulus, without the need to input the entire stress-strain curve.

While it’s a common stance among FEA scholars that linear analysis is not valid when dealing with plastic materials, my experience over the years analyzing countless plastic injection molded components has demonstrated that linear analysis can yield results that align with physical testing.

Nonetheless, it’s crucial to acknowledge that nonlinear FEA generally offers more dependable results when working with plastic materials. However, owing to its efficiency and ease of use, linear FEA can still be a valuable tool, especially during the initial phases of analysis, offering a practical compromise between accuracy and computational resources.

 

If, after perusing this article, you find yourself in doubt regarding the most fitting analysis for your specific application, don’t hesitate to reach out to our seasoned FEA experts at Situs Engineering. We are readily available to engage in a comprehensive discussion about your unique situation and can offer tailored recommendations to guide you in the right direction.